• 平衡二叉树，是一种二叉排序树，其中每一个节点的左子树和和右子树的高度差至多等于1。
• 平衡因子，将二叉树的左子树深度减去右子树深度的值称为平衡因子BF（Balance Factor）。
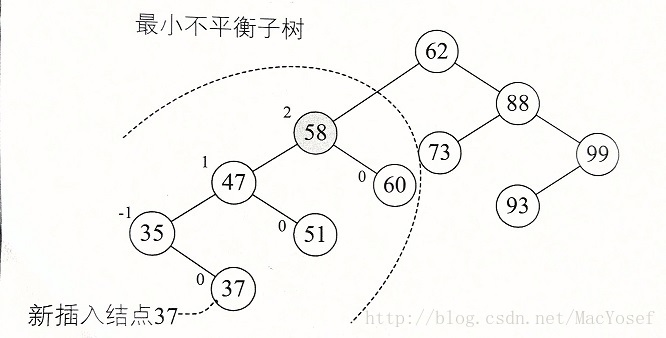
• 最小不平衡子树，距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树。

平衡二叉树 构建

​平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插人一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树，在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点间的链接关系，进行相应的旋转，使之成为新的平衡子树。

a[10]={3,2,1,4,5,6,7,10,9,8} 的构建过程
图解：

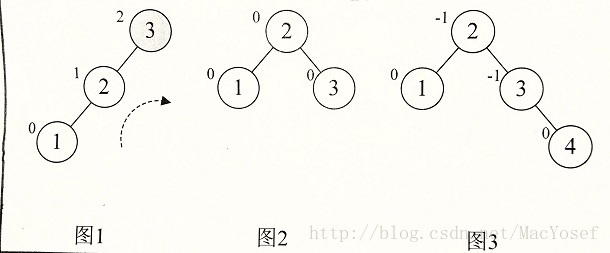
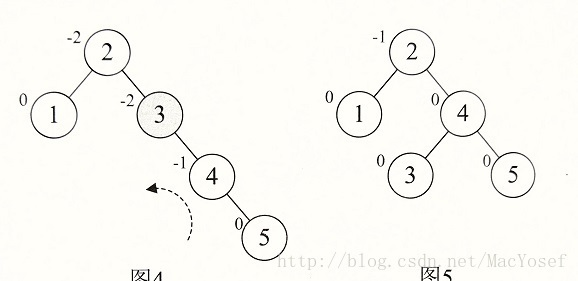
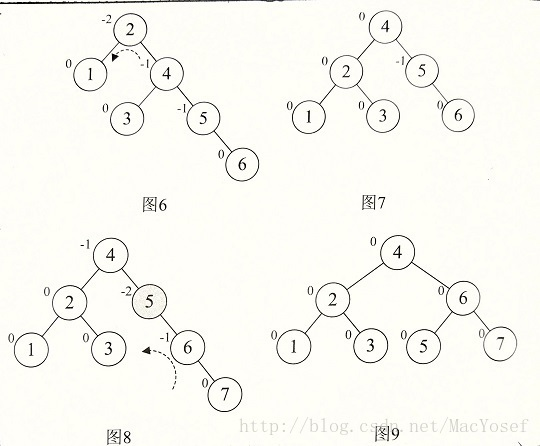
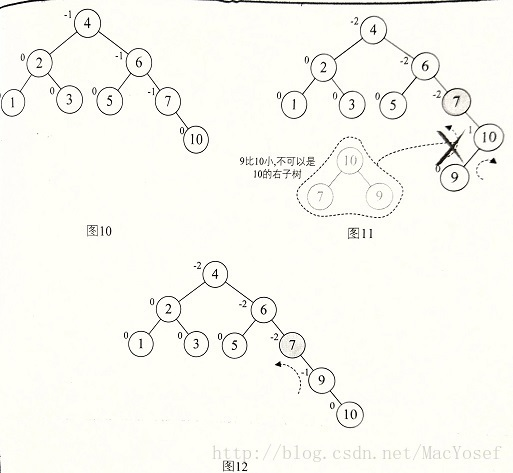
图11不能简单的旋转，仔细观察图就会发现，根本原因在于结点7的BF是-2，而结点10的BF是1，符号不同意。前面的几次旋转，无论左还是右旋，最小不平衡树的根节点与它的子节点的BF符号是相同的。 这就是不能直接旋转的关键。
所以需要先把它们转到符号统一：对结点9和结点10进行右旋，再以结点7位最小不平衡子树进行左旋。

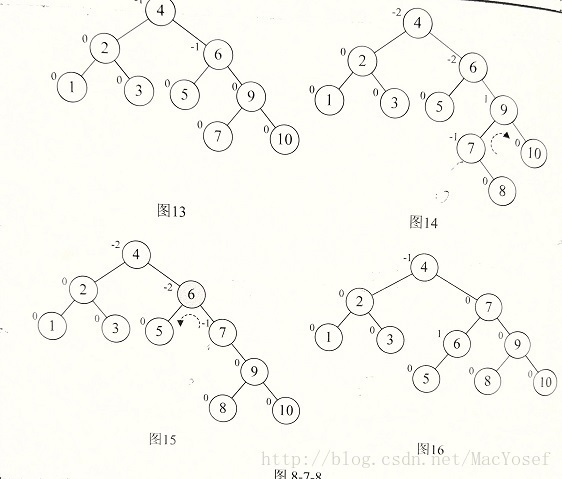
主要算法：

/*二叉树的二叉链表结点结构定义*/
typedef struct BitNode				   /*结点结构*/
{
	int data;                          /*结点数据*/
	int bf;                            /*结点的平衡因子*/
	struct BitNode *lchild,*rchild;    /*左右孩子指针*/
}BitNode,*BiTree;

/*对以P为根的二叉树作右旋处理*/
/*处理之后P指向新的树根结点，即旋转处理之前的左子树的根节点*/
void R_Rotate(BiTree *P)
{
	BiTree L;
	L=(*P)->lchild;
	(*P)->lchild = L->rchild;
	L->rchild=(*P);
	*P =L;
}

右旋图解：

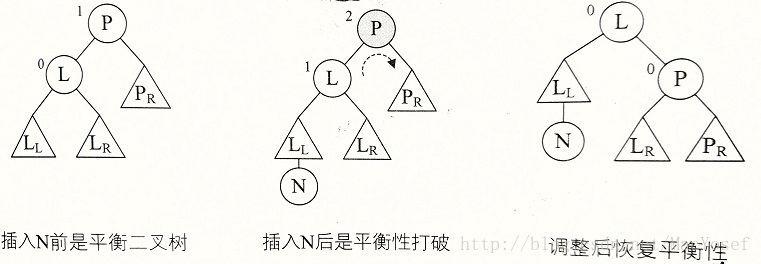
#define LH 1
#define EH 0
#define RH -1
/*对以指针T所指根节点为根的二叉树作左平衡旋转处理*/
/*本算法结束时，指针T指向新的根节点*/
void LeftBalance(BiTree *T)
{
	BiTree L,Lr;
	L=(*T)->lchild;    /*L指向T的左子树根节点*/
	switch(L->bf)
	{    /*检查T的左子树的平衡度，并作相应平衡处理*/
		case LH:   /*新结点插入在T的左孩子的左子树上，作右旋处理*/
			(*T)->bf=L->bf=EH;
			R_Rotate(T);
			break;
		case RH:   /*新结点插入在T的左孩子的右子树上，作双旋处理*/
			Lr = L->rchild;   /*Lr指向T的左孩子的右子树根*/
			switch(Lr->bf)    /*修改T及其左孩子的平衡因子*/
			{
				case LH:
					(*T)->bf = RH;
					L->bf = EH;
					break;
				case EH:
					(*T)->bf = L->bf = EH;
					break;
				case RH:
					(*T)->bf = EH;
					L->bf = LH;
					break;
			}
			Lr->bf = EH;
			L_Rotate(&(*T)->lchild);   /*对T的左子树作左旋平衡处理*/
			R_Rotate(T);               /*对T作右旋平衡处理*/
			break;
	}
}

左平衡旋转图解：

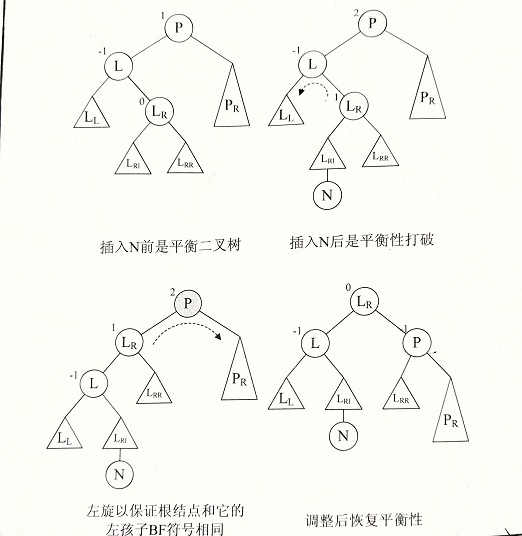
主函数：

//若在平衡的二叉排序树T中不存在和e有相同关键字的结点，
//则插入一个数据元素为e的新结点并返回1，否则返回0。若因插入而使二叉排序树失去平衡，
//则作平衡旋转处理，布尔变量taller反映T长高与否
Status InsertAVL(BiTree *T,int e,Status *taller)
{
	if(!*T)
	{   /*插入新结点，树“长高”，置taller为TRUE */
		*T=(BiTree)malloc(sizeof(BiTNode));
		(*T)->data = e;
		(*T)->lchild=(*T)->rchild = NULL;
		(*T)->bf=EH;
		*taller = TRUE;
	}
	else
	{
		if(e==(*T)->data)
		{   /*树中已存在和e相同关键字的结点则不再插入*/
			*taller=FALSE;
			return FALSE;
		}
		if(e<(*T)->data)
		{   /*继续在T的左子树中进行搜索*/
			if(!InsertAVL(&(*T)->lchild,e,taller))
				return FALSE;
			if(*taller) /*已插入到T的左子树中且左子树高度增加*/
			{
				switch((*T)->bf)   /*检查T的平衡度*/
				{
				case LH:  /*原本左子树比右子树高，需要作平衡处理*/
					LeftBalance(T);
					*taller=FALSE;
					break;
				case EH:  /*原本左右子树等高，现因左子树增高而树增高*/
					(*T)->bf=LH;
					*taller = TRUE;
					break;
				case RH:  /*原本右子树高，现左右子树等高*/
					(*T)->bf = EH;
					*taller = FALSE;
					break;
				}
			}
		}
		else
		{   /*继续在T的左子树中进行搜索*/
			if(!InsertAVL(&(*T)->rchild,e,taller))
				return FALSE;
			if(*taller)
				switch((*T)->bf)
				{
					case LH:
						(*T)->bf=EH;
						*taller = FALSE;
						break;
					case EH:
						(*T)->bf=RH;
						*taller = TRUE;
						break;
					case LH:
						RightBalance(T);
						*taller = FALSE;
						break;
				}
			}
		}
	}
	return TRUE;
}