《Unity Shader入门精要》-冯乐乐 第四章读书笔记
作者博客：http://blog.csdn.net/candycat1992

开始

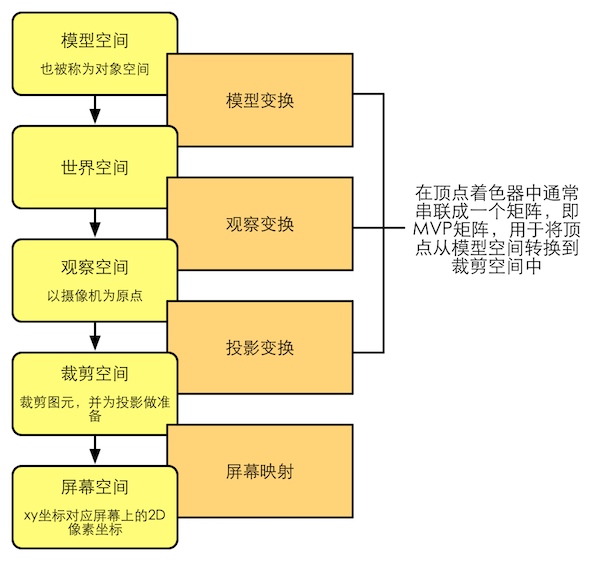
一些重要的空间变换

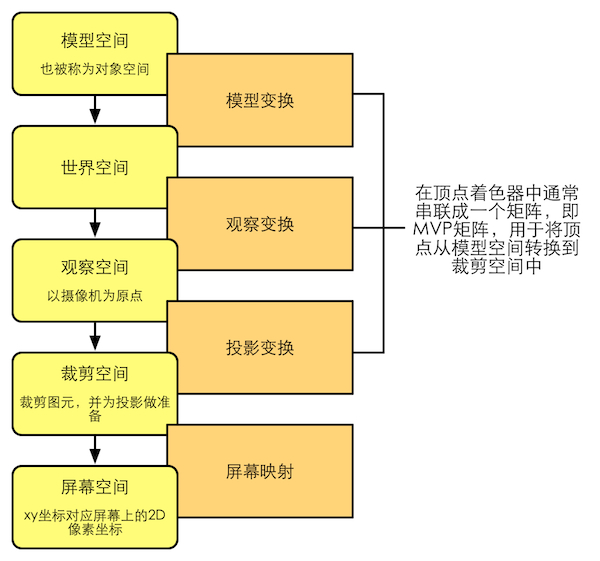
模型空间

模型空间，有时也被称为对象空间（object space）或局部空间（local space）。

每个模型都有自己独立的坐标空间，当它移动或者旋转的时候，模型空间也会跟着它移动和旋转。

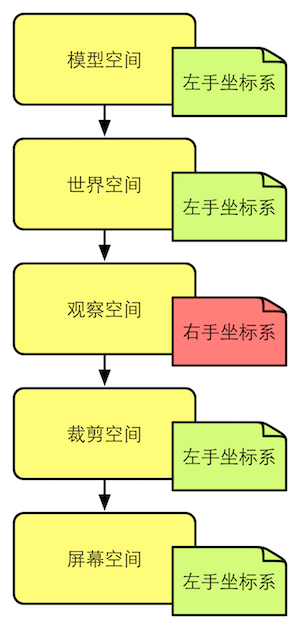
Unity在模型空间中使用的是左手坐标系。模型空间的原点和坐标通常在建模软件中确定好的。

当导入Unity后，可以在顶点着色器中访问到模型的顶点信息。

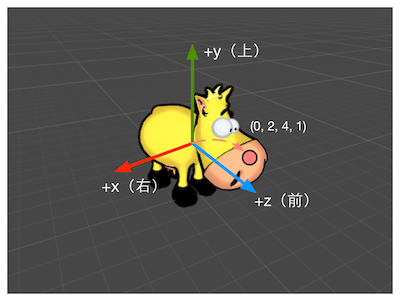
世界空间

在Unity中最大的空间，使用的是左手坐标系。在Unity中我们可以通过调整Transform组件中的Position属性来改变模型的位置，这里的位置指的是相对于这个Transform的父节点（Parent）的模型坐标空间中的原点定义的。

如果一个Transform没有父节点，这个位置就是世界坐标系中的位置。

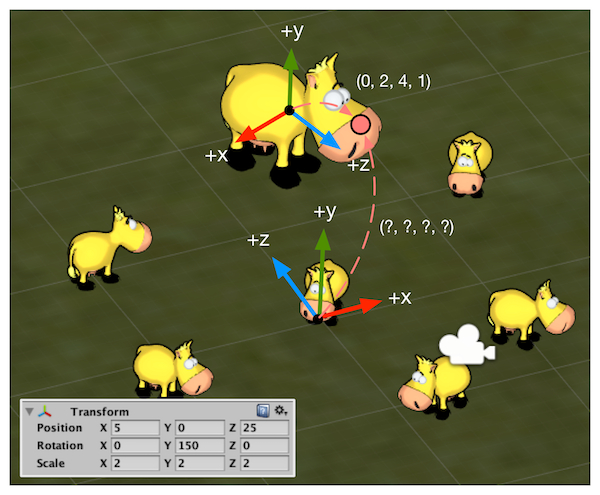
顶点变换的第一步，就是将顶点坐标从模型空间变换到世界空间中。通常称作模型变换

大多数情况下，我们约定变换的顺序就是先缩放，再旋转，最后平移。

根据上图Transform组件的信息构建模型变换的变换矩阵：

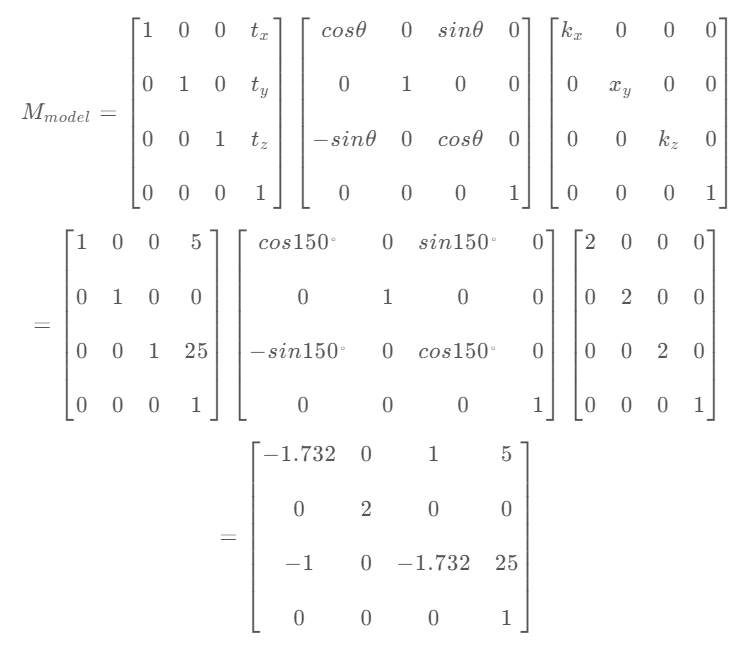
现在可以用它进行模型变换

$P_{world} = M_{model}P_{model}$

观察空间

观察空间也被称为摄像机空间。

在观察空间中，摄像机位于原点。Unity中观察空间的坐标轴：+x轴指向右方，+y轴指向上方，+z轴指向摄像机的后方

观察空间中使用的是右手坐标系，这是符合OpenGL传统的。

注意：观察空间和屏幕空间是不同的。一个是三维，一个是二维。

现在，需要求出从世界空间变换到观察空间的变换矩阵。第一种方法：计算 观察空间的的三个坐标轴在世界空间下的表示

构建出从观察空间变换到世界空间的变换矩阵，再对该矩阵求逆。

$M_{c→p} = \begin{bmatrix} | & | & | & | \\ x_c & y_c & z_c & o_c \\ | & | & | & | \\ 0 & 0 & 0 & 1 \end{bmatrix}$

第二种方法：想象平移整个观察空间，让摄像机位于世界坐标的原点，坐标轴与世界空间的坐标轴对齐（除了z轴，z轴相反）

按照第二种方法，由前面图片的Transform组件，进行逆向变换：将摄像机先按（0，-10,10）平移，回到原点，再按（-30,0,0）旋转，坐标轴对齐。即可求得变换矩阵 M_view

世界空间->观察空间

$P_{view} = M_{view}P_{world}$

裁剪空间


裁剪空间也被称为齐次裁剪空间。使用裁剪矩阵（clip matrix）或者叫做投影矩阵（projection matrix）进行顶点变换。裁剪空间的目标是能都方便地对渲染图元进行裁剪：视锥体内的图元被保留，视锥体外的图元被剔除，视锥体相交的图元会被裁剪。

视锥体有两种类型，这涉及到两种投影类型：透视投影、正交投影。

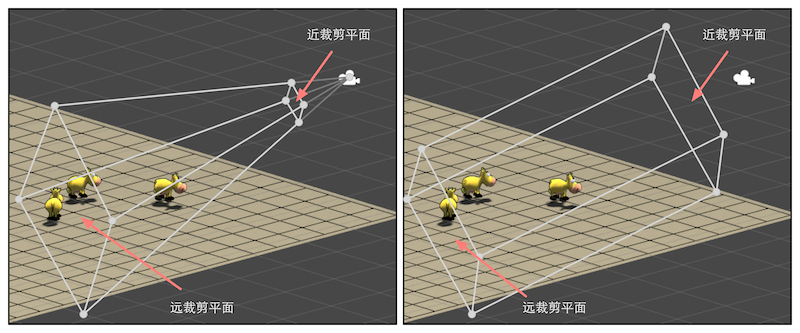
对于透视投影的视锥体来说，想要判断一个顶点是否处于内部是比较麻烦的。因此通过一个投影矩阵把顶点转换到一个裁剪空间中进行裁剪工作。

投影矩阵有两个目的：

首先是为投影做准备。虽然投影矩阵包含了投影二字，但是并没有真正的进行投影工作。真正的投影发生在后面的齐次除法过程中。

其次是对x，y，z分量进行缩放。直接使用视锥体的6个裁剪平面来进行裁剪会比较麻烦。经过投影矩阵的缩放后，可以直接使用w分量作为阈值，如果x，y，z分量都位于这个阈值内，就说明位于裁剪空间内。

透视投影：

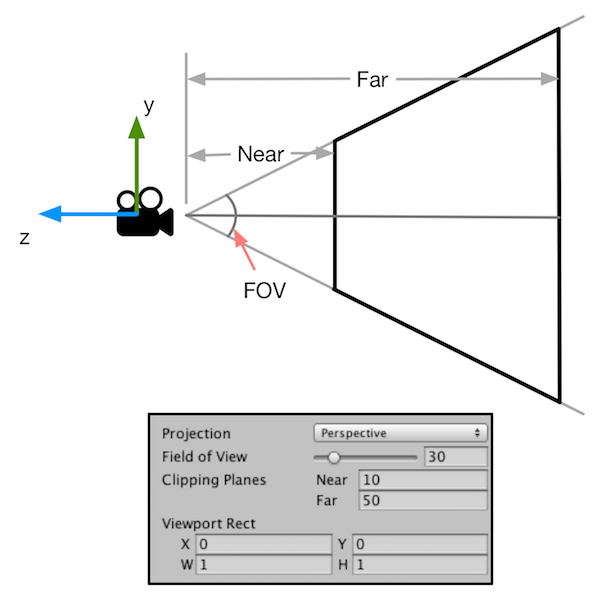
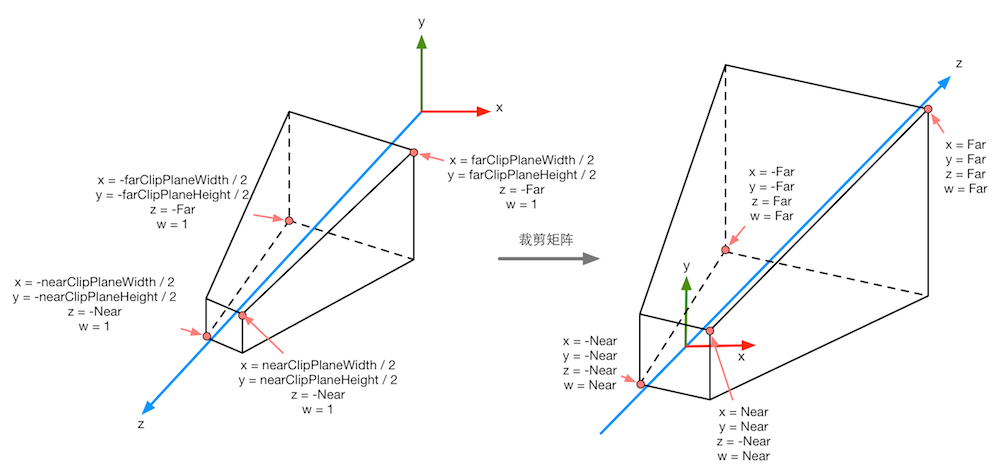
正交投影：

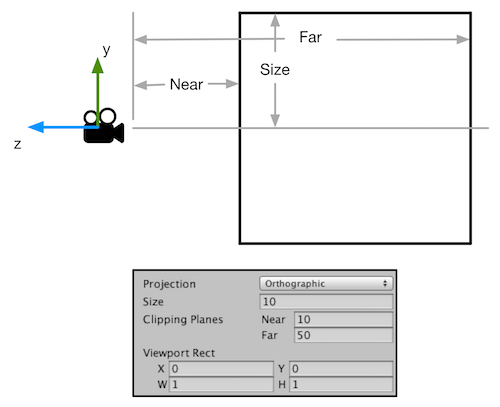
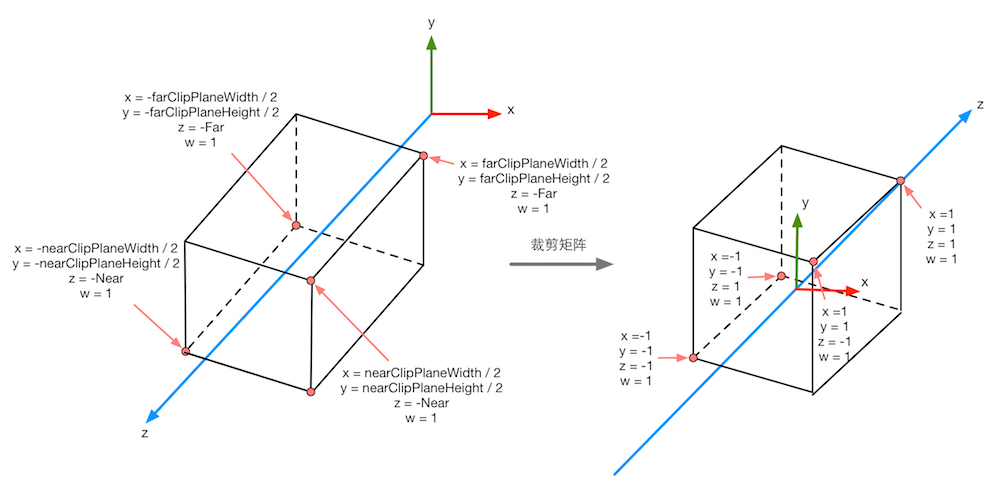
经过变换后，如果一个顶点在视锥体内，那么它变换后的坐标必须满足：

$-w \leq x \leq w$

$-w \le y \le w$

$-w \le z \le w$

任何不满足上述条件的图元都需要被剔除或者裁剪。

屏幕空间

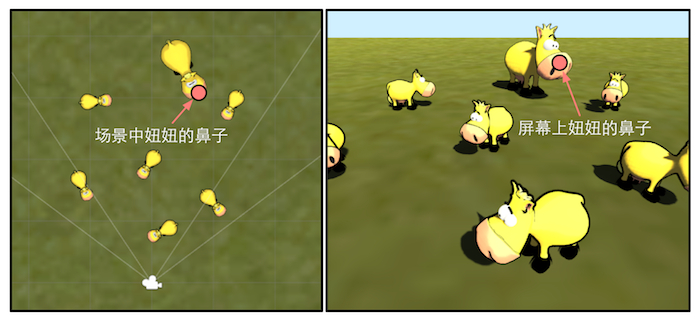
经过投影矩阵的变换后，我们可以进行裁剪操作。当完成了所有裁剪工作后，就需要进行真正的投影了：我们需要把视锥体投影到屏幕空间中。经过这一步变换，我们会得到真正的像素位置。

这一步将顶点从裁剪空间投影到屏幕空间中，来生成对应的2D坐标。这个过程可以理解成两个步骤：

首先进行标准齐次除法(homogenous division)，也称为透视除法。这个步骤就是用齐次坐标系的w分量去除以x、y、z分量。在OpenGL中，我们把这一步得到的坐标叫做归一化的设备坐标（Normalized Device Coordinates，NDC）。

经过透视投影变换后的裁剪空间，经过齐次除法后会变换到一个立方体内。

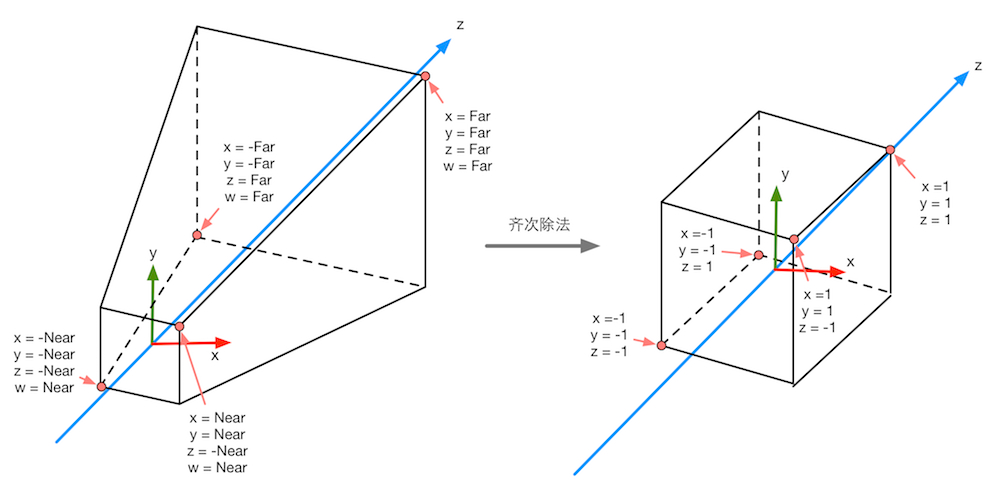
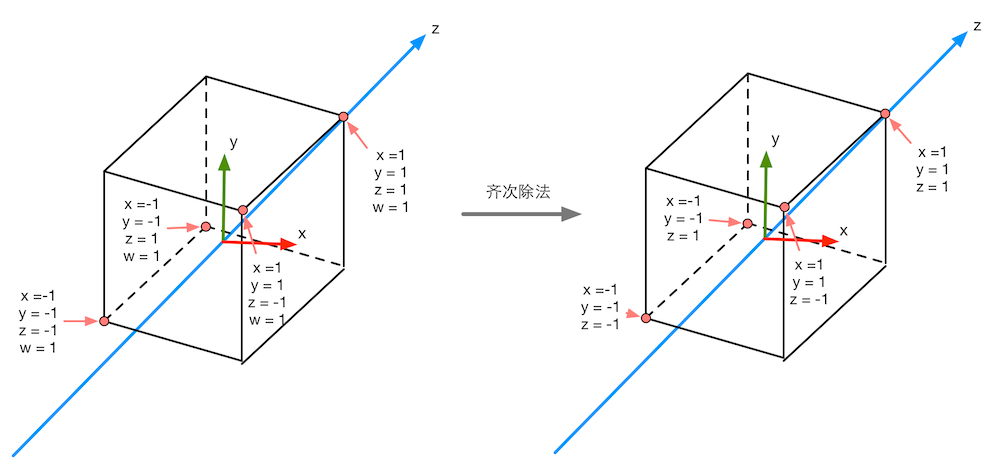
注意：按照OpenGL的传统，这个立方体x、y、z分量的范围都是[-1,1]。但在DirectX这样的API中，z分量的范围是[0,1]。Unity使用的是OpenGL的齐次裁剪空间

经过齐次除法后，透视投影和正交投影的视锥体都变换到一个相同的立方体内。现在可以根据变换后的x和y坐标来映射输出窗口的对应像素坐标。

在Unity中，屏幕空间左下角的像素坐标是（0,0）右上角的像素坐标是（pixelWidth,pixelHeight）。

齐次除法和屏幕映射的过程可以使用下面的公式来总结：

$screen_x = \frac{clip_x \cdot pixelWidth}{2 \cdot clip_w} + \frac{pixelWidth}{2}$

$screen_y = \frac{clip_y \cdot pixelHeight}{2 \cdot clip_w} + \frac{pixelHeight}{2}$

对于z分量，通常用于深度缓冲。一个传统的方式是把 clip_z/clip_w的值直接存进深度缓冲中。

在Unity中，从裁剪空间到屏幕空间的转换是由底层帮我们完成的。顶点着色器只要把顶点转换到裁剪空间即可。

以上就是一个顶点从模型空间变换到屏幕坐标的过程。

完